TRƯỜNG HỢP BẰNG NHAU THỨ BA CỦA TAM GIÁC: GÓC - CẠNH - GÓC (G.C.G)

A. Lý thuyết

1. Vẽ tam giác biết một cạnh và hai góc kề

Bài toán: Vẽ tam giác ABC biết BC = 4cm, ∠B = 60^o, ∠C = 40^o

• Vẽ đoạn thẳng BC = 4cm.

• Trên cùng một nửa mặt phẳng phẳng bờ BC, vẽ các tia Bx và Cy sao cho ∠CBx = 60^o, ∠BCy = 40^o.

Hai tia trên cắt nhau tại A, ta được tam giác ABC.

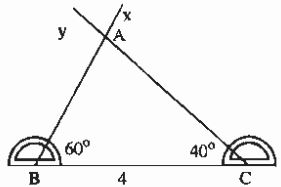
Lưu ý: Ta gọi góc B và góc C là hai góc kề cạnh BC. Khi nói một cạnh và hai góc kề, ta hiểu hai góc này là hai góc ở vị trí kề cạnh đó.

2. Trường hợp bằng nhau góc – cạnh – góc

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

ΔABC và ΔA'B'C' có:

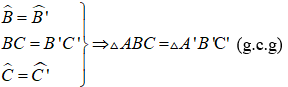
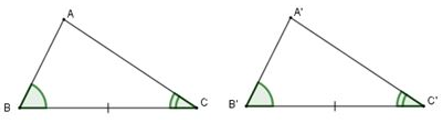
3. Hệ quả

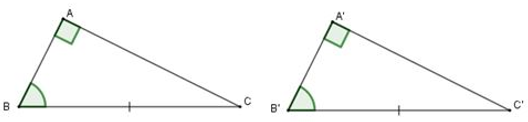
• Hệ quả 1: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Hệ quả 2: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Ví dụ:

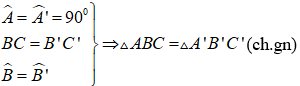
B. Bài tập

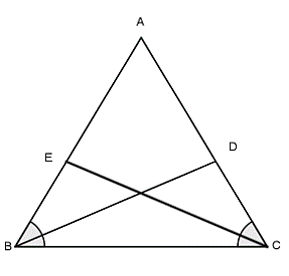
Bài 1: Cho ΔABC có ∠B = ∠C. Tia phân giác của góc B cắt AC tại D. Tia phân giác của góc C cắt AB tại E. So sánh độ dài đoạn thẳng BD và CE.

Lời giải:

Bài 2: Cho tam giác ABC (AB = AC) và I là trung điểm của đáy BC. Dựng tia Cx song song với tia BA sao cho hai tia BA và Cx nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng BC. Lấy một điểm D nào đó trên AB. Gọi E là một điểm nằm trên tia Cx sao cho BD = CE. Chứng minh rằng ba điểm D, I, E thẳng hàng.

Lời giải:

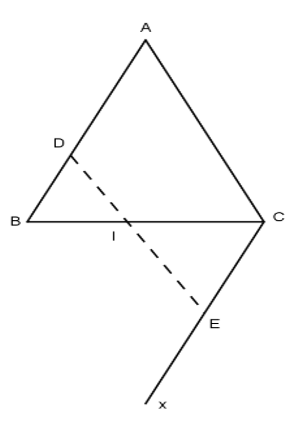
Xét hai tam giác BID và CIE ta có:

BI = IC (I là trung điểm của BC)

∠IBD = ∠ICE (Cx // AB, ∠IBD; ∠ICE hai góc so le trong)

BD = CE (gt)

⇒ ΔBID = ΔCIE (c-g-c)

Nên ∠BID = ∠CIE (hai góc tương ứng bằng nhau)

Hai góc này bằng nhau, chiếm vị trí đối đỉnh, có hai cạnh tương ứng BI và CI nằm trên một đường thẳng.

Vậy D, I, E thẳng hàng

C. Bài tập tự luyện

Bài 1. Cho tam giác ABC. Trên tia đối của tia AB lấy điểm H sao cho AH = AB. Trên tia đối của tia AC lấy điểm K sao cho AK = AC. Một đường thẳng đi qua A cắt các cạnh HK, BC tại D và E. Chứng minh rằng:

a) HK song song BC.

b) A là trung điểm của DE.

Hướng dẫn giải:

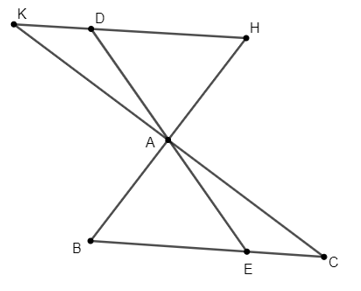
a) Xét DABC và DAHK có:

AB = AH (giả thiết),

ˆCAB=ˆKAH (hai góc đối đỉnh),

AC = AK (giả thiết),

Do đó ∆ABC = ∆AHK (c.g.c).

Suy ra ˆABC=ˆAHK (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong.

Nên HK // BC (dấu hiệu nhận biết).

Vậy HK // BC.

b) Xét ∆ABE và ∆AHD có:

ˆEAB=ˆDAH (hai góc đối đỉnh),

AB = AH (giả thiết),

ˆABE=ˆAHD (vì ˆCAB=ˆKAH),

Do đó ∆ABE = ∆AHD (g.c.g).

Suy ra AE = AD (hai cạnh tương ứng).

Do đó A là trung điểm của DE.

Vậy A là trung điểm của DE.

Bài 2. Điền vào chỗ còn thiếu trong các bước chứng minh sau:

“Xét ∆ABC và ∆MNP có:

.............,

BC = PN.

ˆABC=ˆMNP;

Vậy ΔABC = ∆MNP (g.c.g)

A. AB = MN;

B. ˆACB=ˆMPN;

C. AC = MP;

D. ˆBAC=ˆNMP.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: ΔABC = ∆MNP theo trường hợp góc – cạnh – góc nên hai cặp góc bằng nhau là hai cặp góc kề với cặp cạnh bằng nhau của hai tam giác.

Mà BC = PN và ˆABC=ˆMNP nên cặp góc kề tương ứng còn lại là ˆACB=ˆMPN.

Bài 3. ho góc nhọn xOy, Oz là tia phân giác của góc đó. Qua điểm A thuộc tia Ox kẻ song song với Oy cắt Oz tại M. Qua M kẻ đường song song với Ox cắt Oy tại B. Chọn câu đúng

A. OA > OB; MA > MB

B. OA = OB; MA = MB

C. OA < OB; MA < MB

D. OA < OB; MA = MB

Hướng dẫn giải:

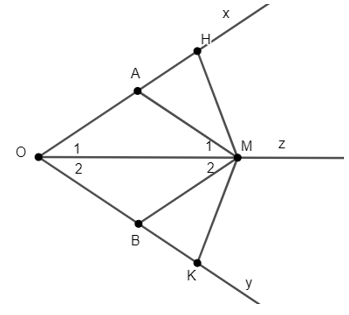
Ta có: ˆM1=ˆO2 (hai góc so le trong)

ˆM2=ˆO1(hai góc so le trong)

ˆO1=ˆO2 (Vì Oz là tia phân giac của)

Do đó: ˆM1=ˆM2

Xét ∆AOM và ∆BOM ta có:

ˆM1=ˆM2 (cmt)

OM chung

ˆO1=ˆO2

Suy ra ∆AOM = ∆BOM (g.c.g)

Do đó: OA = OB; MA = MB (cạnh tương ứng bằng nhau).

Bài 4. Cho ΔABC có ˆB=ˆC. Tia phân giác của góc B cắt AC tại D. Tia phân giác của góc C cắt AB tại E. So sánh độ dài đoạn thẳng BD và CE.

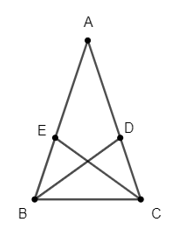
Hướng dẫn giải:

Xét ∆EBC và ∆DCB ta có:

ˆEBC=ˆDCB (gt)

BC là cạnh chung

ˆECB=ˆDBC=12ˆB=12ˆC

Nên suy ra ∆EBC = ∆DCB (g.c.g)

Suy ra BD = CE (cặp cạnh tương ứng bằng nhau).

Bài 5. Cho tam giác ABC có AB = 2,5 cm, AC = 3 cm, BC = 3,5 cm. Qua A vẽ đường thẳng song song với BC, qua C vẽ đường thẳng song song với AB, chúng cắt nhau ở D. Tính chu vi tam giác ACD.

Hướng dẫn giải:

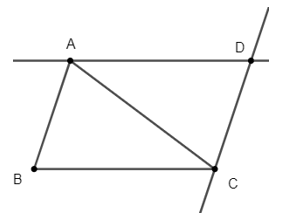
Xét ∆ABC và ∆ACD có:

AC: cạnh chung

ˆBAC=ˆACD (AB // CD)

ˆDAC=ˆACB (AD // BC)

 ⇒ ∆ABC = ∆ADC (g.c.g)

⇒ AB = DC = 2,5 cm

Ta có: ∆ABC = ∆ADC

⇒ BC = AD = 3,5 cm

Chu vi của ∆ACD là:

AC + AD + CD = 2,5 + 3,5 + 3 = 9 (cm)

Vậy chu vi ∆ACD là 9 cm.

Bài 6. Cho đoạn thẳng AB. Qua A vẽ đường thẳng m vuông góc với AB. Qua B vẽ đường thẳng n vuông góc với AB. Qua trung điểm O của AB vẽ một đường thẳng cắt m ở C và cắt n ở D. So sánh các độ dài OC và OD.

Bài 7. Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC ở D. Kẻ DE vuông góc với BC. Chứng minh rằng AB = BE.

Bài 8. Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy

(B, C nằm cùng phía đốivới xy). Kẻ BD và CE vuông góc với xy. Chứng minh rằng:

a) ∆BAD = ∆ACE

b) DE = BD + CE

Bài 9.Cho tam giác ABC. Vẽ ở phía ngoài tam giác ABC các tam giác  vuông tại A là ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng:

a) DM = AH;

b) MN đi qua trung điểm của DE.

Bài 10. Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC ở E, đường thẳng qua E và song song với AB cắt BC ở F. Chứng minh rằng:

a) AD = EF;

b) ∆ADE = ∆EFC;

c) AE = EC.